Le concept de transformation de Fourier est indispensable pour la compréhension du traitement du signal (et à fortiori du traiment de l'image). Du nom d'un mathématicien Français, la transformation de Fourier repose sur le principe suivant : quasiment toutes les fonctions sont décomposables en une somme de cosinus et de sinus à des fréquences différentes. Ainsi, lorsque l'on représente une fonction dans un repère Amplitude/Temps, la transformation de Fourier permet de la voir dans un repère Amplitude/Fréquence. On voit donc les composantes en fréquence d'un signal.



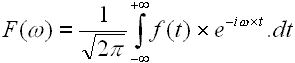
Il est important de savoir que l'on peut repasser à la fonction d'origine à partir d'une transformée de Fourier en appliquant une transformation de Fourier inverse.
Notre intuition nous dit que lorsque nous avons affaire à un signal ou il y a beaucoup de "petits" bruits alors les composantes en hautes fréquences vont être importantes. Ce genre de propriétés permet d'appliquer des filtres sur les fonctions. Ainsi pour adoucir une image (pour enlever le bruit) on applique un filtre passe-bas (c'est un filtre qui ne laisse passer que les basses fréquences, appelé aussi "blur"). Pour conclure, il faut se rendre compte de quelques points importants:
- La tranformée de Fourier d'une fonction permet de voir le signal sous un autre jour. Elle donne des informations qui ne sont pas forcéments triviales sur la fonction.
- Il existe de nombreuses autres transformations, telles que la transformation en Z etc... D'ailleurs la transformation de Fourier possède des désavantages. En effet, pour la calculer, on intègre la fonction sur tout le temps. On perd ainsi complètement l'information temporelle. Ceci ne pose pas de problèmes pour un signal stationnaire.